Анализ напряженно-деформированного состояния трубопровода при воздействии ударной волны с установленным на нем самостабилизатором давления
К. А. МЯГКОВ – инженер-расчетчик 1 категории ООО «ТехПромАрма»
Н. В. ТАННЕНБЕРГ – инженер-конструктор 2 категории ООО «ТехПромАрма»
Р. Ф. ГАФФАНОВ – к.т.н., ООО «Инженерно-расчетная компания «Проект»
Д. Ю. СЕРИКОВ – к.т.н., доцент РГУ нефти и газа имени И. М. Губкина
В статье промоделировано влияние гидравлического удара на трубопроводную систему, проведена оценка напряженно-деформированного состояния участка трубопровода, предложена методика оценки динамического влияния среды на прочность трубопровода.
Трубопроводные системы применяются для транспортировки различных сред: газовых, одно- и двухфазных жидкостных. Рассмотренная в данной работе жидкая среда способна оказывать динамическое воздействие на трубопровод – гидравлический удар.
Существуют множество работ, посвященных исследованию негативных последствий от гидравлического удара [1,2,3]. В данных работах были рассмотрены величины гидравлического удара и последствия влияния гидравлического удара на трубопроводы, без рекомендаций по их устранению. В свою очередь, авторами в работе [4] была предложена конструкция стабилизатора давления и проведен анализ влияния ее на величину гидравлического удара в трубопроводе. В данной работе был проведен численный эксперимент с анализом НДС трубопровода с простой геометрией, с установленным на нем устройством диссипации гидравлического удара в системах (самостабилизатор).
Эксперимент был выполнен при помощи программного комплекса ANSYS LS-DYNA. Цель расчета – определение величин и амплитуд пульсации приведенных напряжений в стенке трубопровода под действием динамической нагрузки от внутренней среды. Согласно работе [4] приведенные напряжения следует рассматривать в опасных сечениях. Под опасным сечением подразумевается сечение трубопровода, в котором время динамического воздействия среды на стенки трубопровода наибольшее (место непосредственного возникновения гидравлического удара; сечение трубопровода, расположенное за самостабилазотором давления, т.е. с противоположной стороны от места возникновения гидравлического удара).
В эксперименте были рассмотрены две расчетные схемы:
- трубопровод без дополнительной защиты от гидравлического удара;
- трубопровод, защищенный самостабилизатором давления.
В расчете приняты следующие условия и допущения:
- расчет выполнен при линейно-упругом поведении материала в рамках закона Гука п.1.2.16 [5], в отсутствии пластических деформаций и разрушения, такая постановка задачи справедлива для рассматриваемого диапазона давлений, при котором верхнее (максимальное) значение абсолютного давления за все время расчета не превышает согласно [6]:

- для описания поведения материала трубопровода использовалась упругая изотропная модель, не учитывающая локальных аномалий структуры, в том числе дислокаций. Согласно техническим условиям [11] на самостабилизатор давления, рассматриваемый в работе [4], материал для трубопровода подбирался в соответствии с выбранным исполнением самостабилизатора, а именно – сталь 08Х18Н10Т. Характеристики материала были заданы при помощи карты *MAT_ELASTIC со следующими величинами:
– Плотность материала [ρ] – 7850 кг/м3;
– Модуль упругости E – 205 ГПа;
– Коэффициент Пуассона ν– 0,3.
- расчетная область представлена частью трубопровода 14х2 длиной 100 мм (рис. 1);
- рассматриваемое сечение, в котором определялись приведенные напряжения в стенке трубопровода от динамического воздействия среды в обоих вариантах расчетных схем, равноудалено от заделок на 50 мм, во избежание влияния границ расчетной области;
- в качестве граничных условий для кривых нагружения от влияния среды в переменных «давление – время» были приняты графики изменения абсолютного давления, полученные в работе [4] и представлены на рисунках (рис. 3 и 4). Трубопровод на торцах жестко закреплен. Общий вид расчетной области с установленными граничными условиями показан на рис. 2;
- согласно критерию Куранта – Фридрихса – Леви (CFL, условие устойчивости явного численного расчета [12]), минимальный шаг по времени определялся как:

- влияние силы тяжести в расчете не учитывалось.
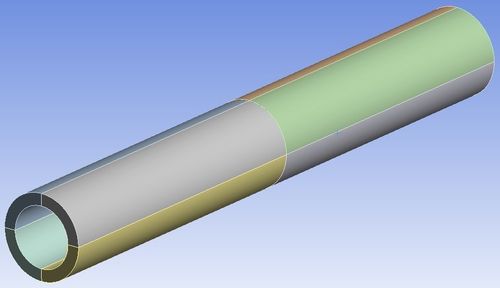
Рис. 1. Общий вид расчетной области
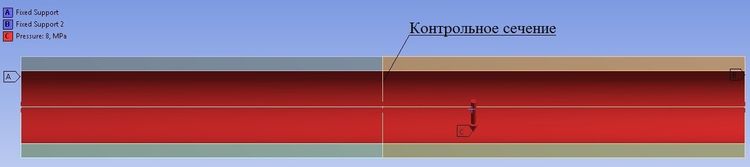
Рис. 2. Общий вид расчетной области с установленными граничными условиями для расчета преднагруженного состояния
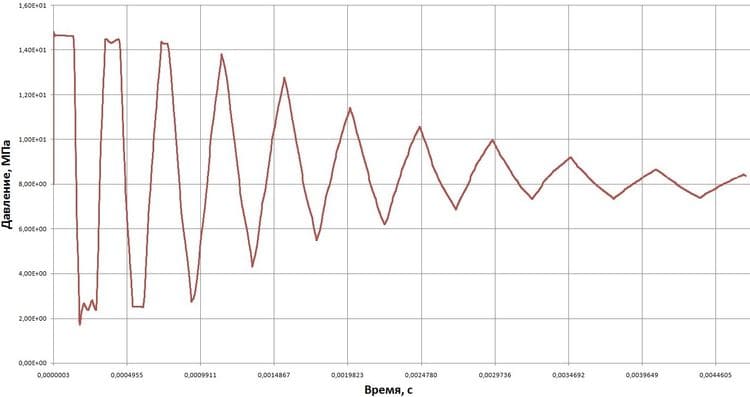
Рис. 3. Кривая нагружения от изменения абсолютного давления для трубопровода без дополнительной защиты от гидравлического удара
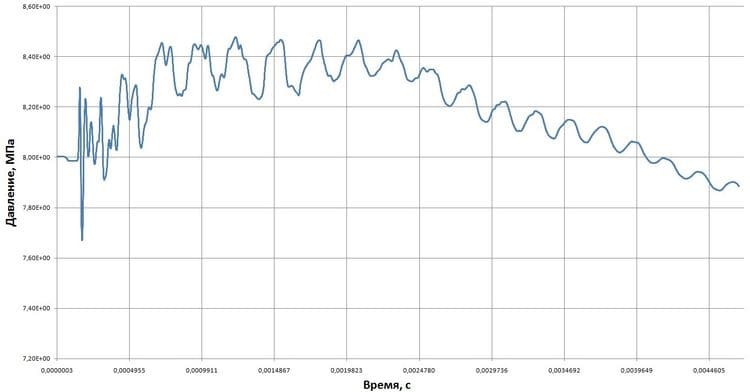
Рис. 4. Кривая нагружения от изменения абсолютного давления для трубопровода, защищенного самостабилизатором давления
Размерность конечно-элементной сетки в обоих вариантах расчетных схем составила 96000 элементов и 110000 узлов. Конечно-элементная сетка представлена на рис. 5.

Рис. 5. Конечно-элементная сетка
Для получения достоверных результатов динамического анализа необходимо предварительно провести расчет преднагруженного состояния. Цель данного расчета – определение перемещений, деформаций и напряжений в узлах и элементах рассматриваемой части трубопровода при статическом нагружении от давления среды. Решение получено при помощи программного комплекса ANSYS LS-DYNA в неявной постановке.
Результаты статического расчета напряжений и деформаций с использованием карт *INITIAL_STRESS_SOLID и *INITIAL_STRAIN_SOLID соответственно, а также новые координаты узлов модели, были учтены в динамическом анализе (рис. 6 и 8, участок 1).
Ниже представлены результаты динамического анализа прочности трубопровода для схемы без дополнительной защиты от гидравлического удара (рис. 6), и для схемы трубопровод, защищенный самостабилизатором давления (рис. 8).
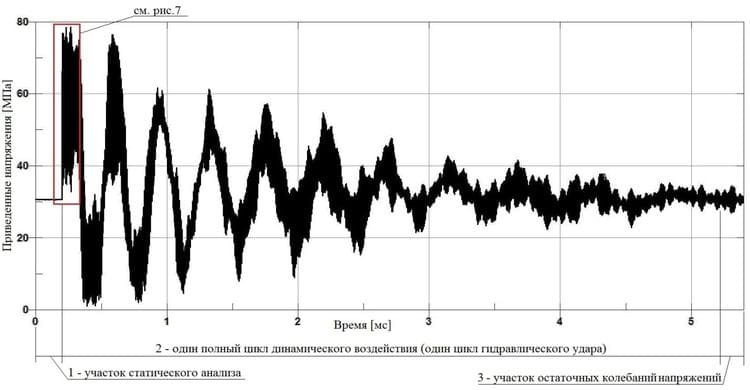
Рис. 6. График изменения приведенных напряжений в стенке трубопровода без дополнительной защиты от гидравлического удара, вызванных динамическим воздействием среды
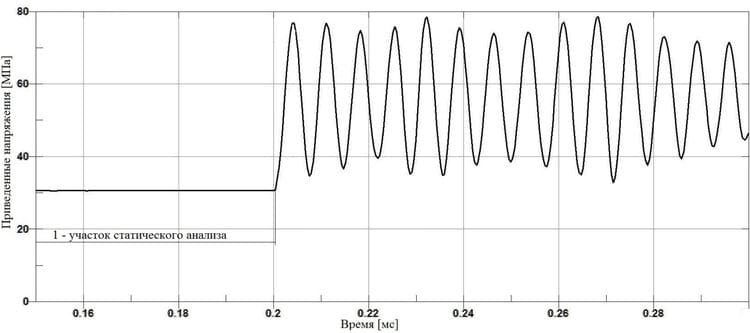
Рис. 7. График изменения приведенных напряжений в стенке трубопровода без дополнительной защиты от гидравлического удара, вызванных динамическим воздействием среды
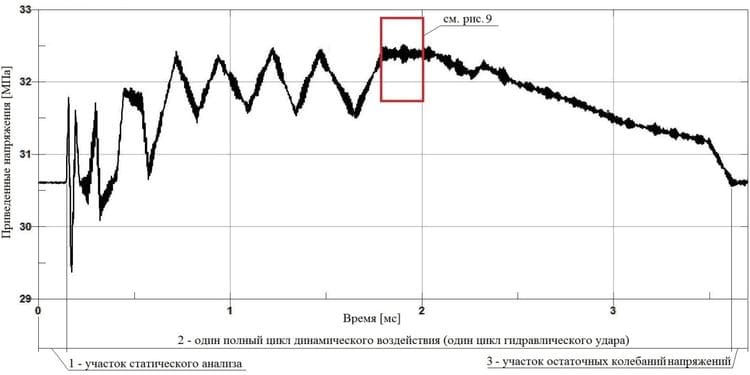
Рис. 8. График изменения приведенных напряжений в стенке трубопровода, защищенного самостабилизатором давления, вызванных динамическим воздействием среды
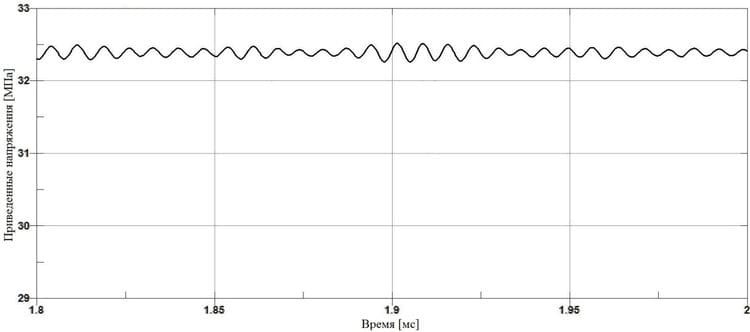
Рис. 9. График изменения приведенных напряжений в стенке трубопровода, защищенного самостабилизатором давления, вызванных динамическим воздействием среды
Как видно из графиков на рис. 6 и 7, упругие волны напряжений, пробегающие по всей толщине стенки трубопровода, имеют две основные гармоники. Причем первая из них имеет период колебаний 0,0072 мс, что соответствует частоте 139 кГц, а вторая, более выраженная, имеет период и частоту явно совпадающие с периодом и частотой колебания нагрузки (частота пульсации гидравлического удара на рассматриваемом участке трубопровода) и равные 0,346 мс и 2,9 кГц соответственно. Пиковое значение приведенных напряжений для схемы трубопровода без дополнительной защиты от гидравлического удара составило 78,7 МПа, что превысило начальный уровень напряжений в статическом состоянии на 48,1 МПа. Максимальный размах напряжений при частоте 139 кГц составил 53,6 МПа.
Наибольший интерес представляет собой именно первая гармоника в плане рассмотрения процесса накопления усталостных повреждений. Столь частое изменение значения приведенного напряжения с большой амплитудой может привести к возникновению микротрещин на поверхности стенки трубопровода, развитие которых, впоследствии, приведет к разрушению конструкции.
Подобный анализ схемы трубопровода, защищенного самостабилизатором давления (рис. 8 и 9) показал аналогичное поведение пульсации напряжений в стенке трубопровода с частотой 139 кГц. При этом пиковое значение приведенных напряжений составило 32,5 МПа и показало увеличение, по сравнению с начальным уровнем напряжений в статическом состоянии, на 1,9 МПа, а максимальный размах напряжений при частоте 139 кГц составил 1,2 МПа.
Сравнивая результаты анализа напряженно-деформированного состояния обеих схем можно заключить, что увеличение уровня напряжений, по сравнению со статическим состоянием, для трубопровода, защищенного самостабилизатором давления в 25 раз меньше, чем для трубопровода без дополнительной защиты от гидравлического удара.
Дальнейшей целью исследования будет нахождение накопленных усталостных повреждений в трубопроводе от одного цикла воздействия гидравлического удара с учетом остаточных колебаний напряжений, основанного на результатах математического моделирования, показанного в данной статье.
ЛИТЕРАТУРА:
- Сериков Д. Ю., Ясашин В. А., Гаффанов Р. Ф. Сравнительный анализ статической прочности прямозубого и косозубого поверхностноармированного вооружения. «Управление качеством в нефтегазовом комплексе». №4, 2013 г., ISSN 0130-3872 с. 31–35.
- M. Giot, H. M. Prasser, F. Castrillo, A. Dudlik, G. Ezsol,J. Jeschke, H. Lemonnier, A. Rubbers, I. Tiselj, W. Van Hove, S. Potapov. TWO-PHASE FLOW WATER HAMMER TRANSIENTS AND INDUCED LOADS ON MATERIALS AND STRUCTURES OF NUCLEAR POWER PLANT (WAHALOADS) KFKI – ATOMIC ENERGY RESEARCH INSTITUTE – HUNGARIA 2004.
- S. D. Saemi1, M. Raisee2, M. J. Cervantes3 and A. Nourbakhsh4 Computations of Laminar and Turbulent Water Hammer Flows.
- К. А. Мягков, Н. В. Танненберг, В. А Пестунов, Р. Ф. Гаффанов+. Гидродинамический анализ эффективности работы самостабилизатора давления в условиях возникновения и распространения гидравлического удара.
- ПНАЭ Г-7-002-86. Нормы расчета на прочность оборудования и трубопроводов атомных энергетических установок. М.: Энергоатомиздат. 1989.
- Г. С. Писаренко, Н. С. Можаровский. Уравнения и краевые задачи теории пластичности и ползучести. Справочное пособие. «Наукова Думка», Киев, 1981.
- Л. Д. Ландау, Е. М. Лифшиц. Механика сплошных сред. Гидродинамика и теория упругости. ОГИЗ Государственное издательство технико-теоретической литературы. Москва, 1944.
- LS-DYNA. Theory Manual.
- Зенкевич, О. Метод конечных элементов в технике / пер. с англ. под ред. Б. Е. Победри. – М.: Мир, 1975.
- Сегерлинд, Л. Применение метода конечных элементов / под ред. Б. Е. Поберди. – М.: Мир, 1979. – с. 392.
- Технические условия ТУ 3790-001-78976334-2012 «Самостабилизатор давления Технические условия».
- R. Courant, K. Friedrichs, H. Lewy Über die partiellen Differenzengleichungen der mathematischen Physik // Mathematische Annalen. – 1928. – Т. 100, № 1. – с. 32–74.


