Исследование динамики системы оптимального управления трубчатой печью при различных критериях управления
Л. Х. ЕЛЬМУРЗАЕВА – инженер отдела математического моделирования ООО «НПА Вира Реалтайм»
Ю. Б. ГЕРШКОВИЧ – к.т.н., доцент кафедры АТП РГУ (НИУ) нефти и газа им. И. М. Губкина
В настоящее время основными путями технического прогресса в нефтепереработке являются увеличение мощности и повышение экономической эффективности технологических установок, снижение себестоимости целевых продуктов и улучшение качества товарных продуктов. Для атмосферной вакуумной трубчатой (АВТ) установки качество и количество получаемых продуктов, а также технико-экономические показатели всей установки в значительной степени зависят от теплового и технологического режимов трубчатой печи.
Трубчатые печи являются важнейшим оборудованием большинства технологических установок в нефтеперерабатывающей, нефтехимической и химической промышленности. В связи с этим особую значимость приобретает задача оптимального управления режимами трубчатых печей. При автоматическом управлении процессом горения являются актуальными две задачи:
- Поддержание температуры продукта на выходе печи;
- Экономия топлива.
Предлагаемая система управления содержит блок идентификации математической модели технологического процесса и блок оптимизации, исследующий систему оптимального управления по двум критериям:
- Динамическому интегральному критерию для синтеза оптимальной системы стабилизации;
- Статическому критерию минимизации расхода топлива.
Для каждого из рассматриваемых подходов составлены алгоритмы и программы в пакете Matlab.
Для разработки и качественной настройки систем автоуправления, как правило, необходимо знать передаточную функцию объекта управления (ОУ). Типичной является ситуация, когда в качестве исходных данных для определения передаточной функции имеется экспериментальная запись реакции ОУ на входное воздействие известной формы.
Определение передаточной функции (математической модели) ОУ и вычисление ее параметров по записанной кривой разгона объекта является задачей математического моделирования и идентификации математической модели. [1]
Исходным материалом для составления математической модели объекта являются экспериментальные данные изменения температуры в зависимости от расхода топлива (степени открытия исполнительного механизма) в трубчатых печах П-1 на установке АВТ с производительностью 3 млн. тонн в год. Идентификация параметров модели проведена в модуле ident математического пакета Matlab. Для загрузки входных и выходных данных необходимо выбрать тип данных (Time domain), ввести имена данных: название входных данных в строке Input, а выходных – в Output. На рис.1 красным цветом показана последовательность действий.
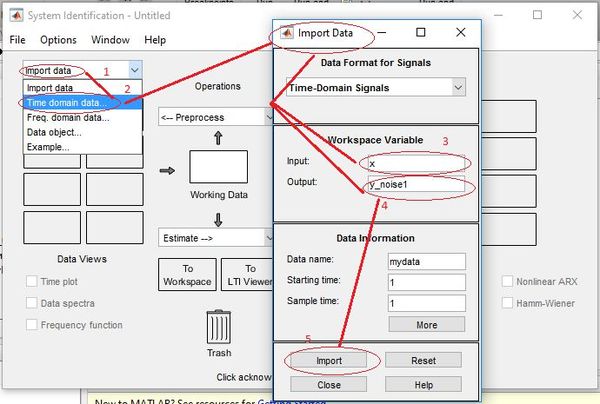
Рис. 1. Окно ввода экспериментальных данных
В результате расчетов получена передаточная функция трубчатой печи следующего вида:
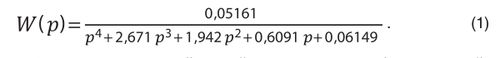
Сравнение полученной кривой разгона по идентифицированной модели с заданной кривой разгона объекта показывает высокую точность по динамическим характеристикам (рис. 2).
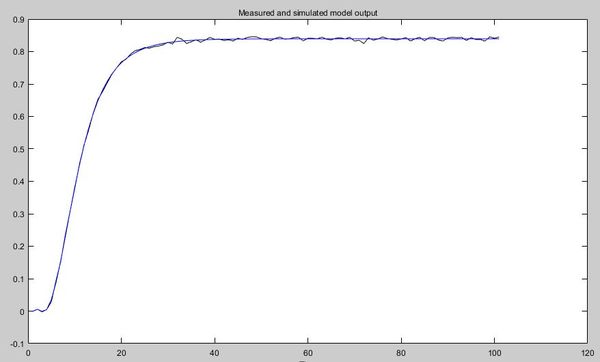
Рис. 2. Кривые разгона технологического объекта и идентифицированной модели
Схема контроля и регулирования работы трубчатых печей предусматривает поддержание определенных параметров в заданных пределах согласно требованиям технологического регламента и безопасной эксплуатации производства. Наиболее важным параметром регулирования в трубчатых печах является температура сырья на выходе из печи. [2]
Для управления трубчатыми печами применяются системы, в алгоритме функционирования которых предписано поддержание на заданном уровне температуры сырья на выходе из печи. Таким образом, рациональная система управления тепловым или технологическим режимами трубчатых печей должна стабилизировать требуемую температуру в печи и находить необходимые соотношения для оптимального расхода топлива согласно экономическим требованиям. [3]
Следовательно, при оптимальном управлении технологическим процессом ставится задача оптимизации критерия управления объектом при ограничениях на сырье, минимизации энергетических затрат и загрязнения окружающей среды. К этим задачам применяется математический аппарат теории оптимального управления, который опирается на формулировку и аналитическую запись критерия управления, и технологические ограничения в виде системы управления и неравенств.
При решении динамических задач применяется интегральный критерий качества, характеризующий энергетические потери на функционирование и управление системы. Математической моделью такого критерия является квадратичный критерий управления.
Процедура аналитического конструирования регулятора предполагает синтез регулятора, минимизирующего интегральный квадратичный критерий с учетом ограничений, представляющих собой систему дифференциальных уравнений, описывающих математическую модель технологического объекта. Критерием управления является минимизация функционала качества:
![]()
Поставленная задача является обобщенной задачей Лагранжа на условный экстремум, для ее решения может быть применен метод вариационного исчисления.
Т.к. объект управления представляет собой технологический объект с нелинейной статической характеристикой с ярко выраженным экстремумом, динамика которого описывается дифференциальным уравнением 4-го порядка, то для решения статической задачи оптимизации используется экстремальный регулятор с запоминанием минимума.
Структурная схема печи как объекта управления представлена на рис. 3.
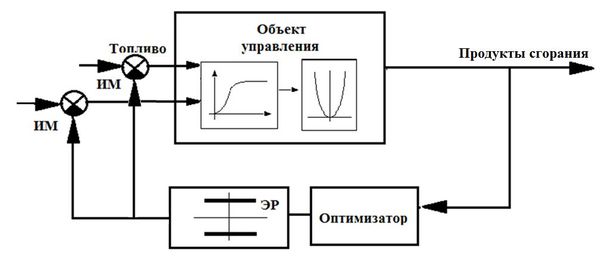
Рис. 3. Структурная схема автоматической системы оптимизации в трубчатой печи
При оптимизации трубчатых печей задача управления может быть сформулирована следующим образом: отклонение температуры сырья на выходе трубчатой печи ΔT не должно превышать заданной по технологии величины TH, т.е.:
![]()
При этом затраты на экономический показатель, т.е. затраты на получение целевого продукта заданного качества, должен быть минимальным:

Для решения задачи стабилизации необходимо рассмотреть систему автоматического регулирования трубчатой печи, структурная схема которой представлена на рис. 4.
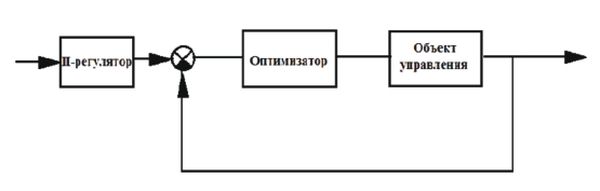
Рис. 4. Замкнутая система с регулятором-оптимизатором
Дифференциальное уравнение трубчатой печи имеет вид:

Переходная характеристика системы представлена на рис. 5.
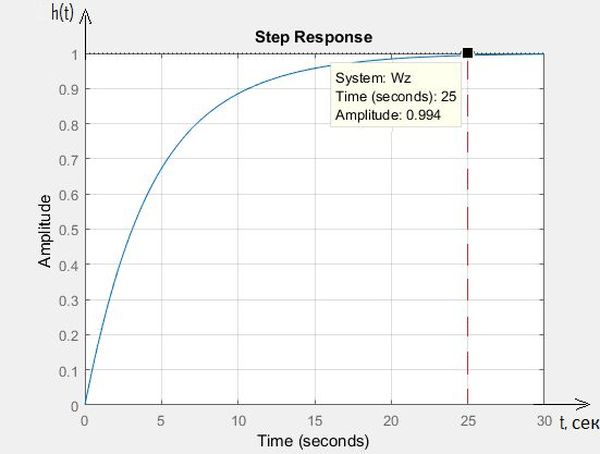
Рис. 5. Переходная характеристика системы
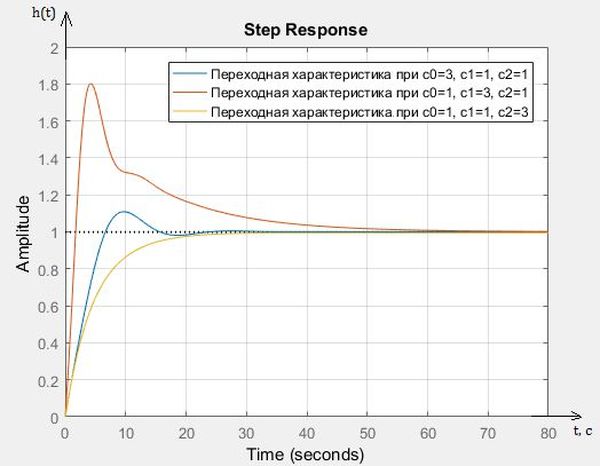
Рис. 6. Переходные характеристики замкнутой системы
Время регулирования переходного процесса отмечено красным цветом и равно tP = 25 секунд.
Далее рассмотрено влияние весовых коэффициентов в критерии управления на показатели качества замкнутой системы.
В таблице 1 приведены сводные значения соответствующих коэффициентов и показателей качества. Переходные характеристики замкнутой системы при различных весовых коэффициентах представлены на рис. 6.
Таблица 1. Показатели качества процесса при различных весовых коэффициентах
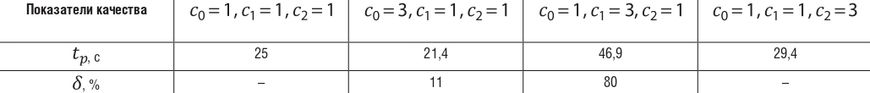
Проанализировав данные таблицы 1, можно сделать выводы о том, что время регулирования tP будет минимальным при увеличении весового коэффициента C0 динамической ошибки x1, однако в данном случае появляется перерегулирование.
При усилении влияния весового коэффициента C1 скорости изменения динамической ошибки x2 показатели качества становятся наихудшими из всех представленных. Перерегулирование переходного процесса δ достигает 80%, а tP увеличивается почти в 1,5–2 раза по сравнению с временем регулирования в остальных случаях.
Также при увеличении весового коэффициента C2 сигнала управления U незначительно увеличивается tP при сопоставлении со случаем равенства всех весовых коэффициентов.
Начальным этапом проектирования системы экстремального регулирования является поиск экстремальных статических характеристик объектов управления. Известно два следующих метода определения статических характеристик:
- Аналитический;
- Экспериментальный.
Для получения статических характеристик экспериментальным методом требуется проведения экспериментов на объекте, что не всегда бывает возможно во время функционирования технологического процесса. Аналитический метод в свою очередь предоставляет возможность находить статические зависимости на стадии проектирования, а также учитывать их в дальнейшей работе. Из литературы известна экстремальная характеристика «топливо-коэффициент избытка воздуха» (рис. 7). [2]
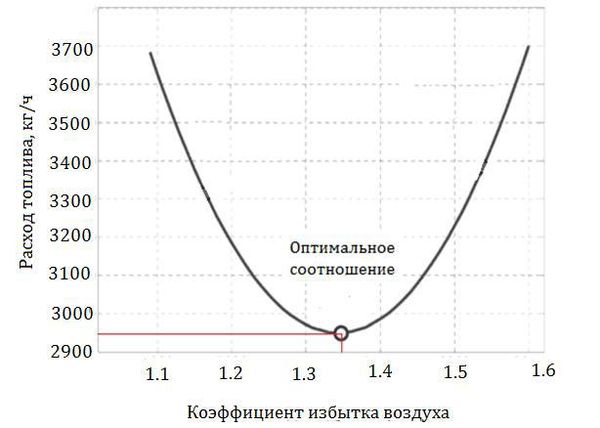
Рис. 7. Экстремальная характеристика «топливо-воздух»
Проведенные исследования позволили сделать следующие выводы: при увеличении коэффициента избытка воздуха происходит уменьшение расхода топлива. Однако это происходит до определенного момента. Когда количество подаваемого воздуха достигает и превышает значение 1,35, количество расходуемого топлива начинает увеличиваться. На первый взгляд кажется, что можно рассчитать это значение и поддерживать работу трубчатой печи в данной точке, чтобы расход топлива был минимальным и экономическая эффективность увеличилась. Но в реальных условиях невозможно поддерживать работу процесса в точке минимума, поскольку точка нестабильна. Характеристика начинает дрейфовать в силу разных причин: из-за налета может меняться режим теплопередачи и теплообмена, случайным образом может меняться качество топлива и т.д.
Применение системы управления горением топлива, предложенной в работе, направлено на разработку энергоэффективных и экономичных методов сжигания топлива. Для ведения процесса горения в экономичном режиме необходимо обеспечить достаточное количество кислорода в любой точке пламени, поэтому практически воздуха подается больше, чем это необходимо для горения.
Значительное увеличение количества воздуха приводит к росту потерь тепла с уходящими топочными газами, а чрезмерное снижение количества воздуха увеличивает потери вследствие неполноты сгорания. Правильность выбора коэффициента избытка воздуха определяется экономичностью процесса горения. [4]
При решении задачи аналитического конструирования регуляторов (АКР) было найдено значение расхода топлива Q=3130 кг/ч, обеспечивающего требуемую температуру на выходе. Однако данное значение расхода не является минимальным для допустимого режима работы печи, как это видно их экстремальной характеристики «топливо-воздух» трубчатой печи (рис. 7).
На рис. 8 представлена блок-схема регулятора.
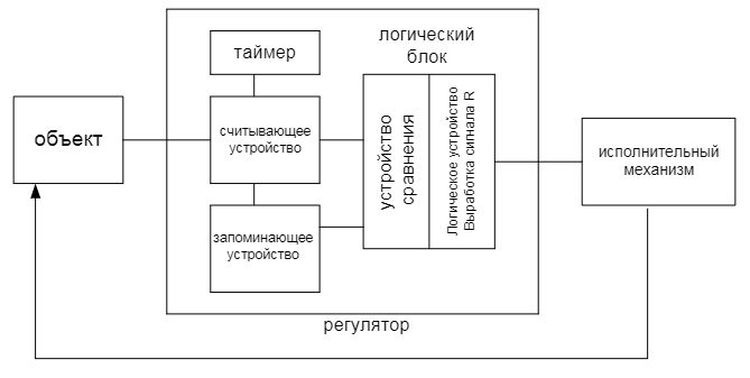
Рис. 8. Блок-схема экстремального регулятора
Модель системы экстремального управления реализована в среде Simulink. Экстремальная статическая характеристика трубчатой, имеющая симметричную зависимость относительно экстремума, задается с помощью блока «ExtremeObjectForm1». Динамическая часть объекта управления формируется из стандартных блоков Simulink. Блок «Actuator» в виде интегратора со сбросом используется в качестве исполнительного механизма (ИМ).
В модель экстремального регулятора (рис. 9) входит элемент сравнения «MinMax Running Resettable», который задает условие переключения и запоминает минимум, сигнум-реле, реализованное на J-K триггере, работающем в режиме T-триггера и блок сигнатуры sign, который переключает направление вращения вала ИМ. При помощи элементов DetectDecrease, Memory1 и вспомогательных блоков для преобразования типов данных и выполнения логических операций осуществляется запоминание только уменьшающегося значения и сброс запоминающего устройства при реверсе.
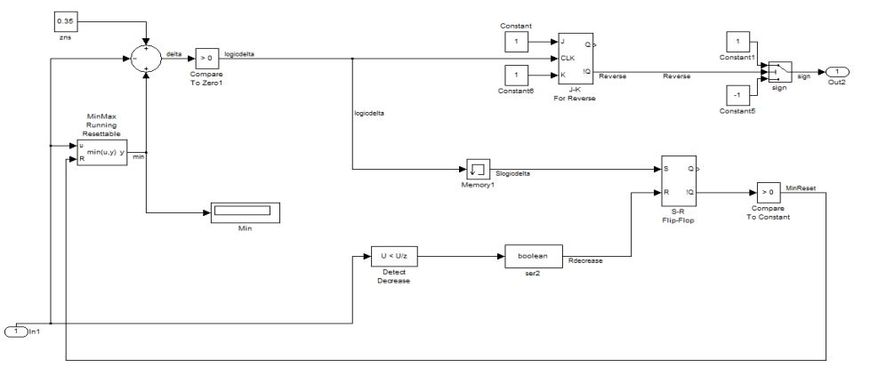
Рис. 9. Модель экстремального регулятора в среде Simulink
На рис. 10 представлена фазовая траектория экстремальной системы управления процессом горения.
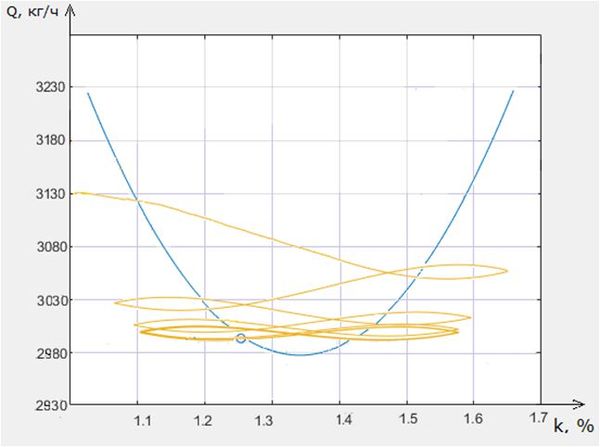
Рис. 10. Фазовая траектория экстремальной системы управления процессом горения
На графике видно, что автоколебания останавливаются около значения расхода топлива 2970 кг/ч. Следовательно, расход топлива в сравнении с расходом, найденным при расчете методом АКР, уменьшается на Q=160 кг/ч. Значит, возрастает экономическая эффективность вследствие уменьшения затрат на топливо.
ВЫВОДЫ:
В статье рассмотрен метод расчета передаточной функции трубчатой печи на основе экспериментальных данных в математическом пакете Matlab и разработан алгоритмы для решения задач оптимального управления по динамическому интегральному критерию для синтеза оптимальной системы стабилизации и статическому критерию минимизации расхода топлива. Применение пакета Matlab и его приложения Simulink для расчетов обосновано современными требованиями к простоте и быстроте решения сложных математических задач. Поиск минимума расхода топлива в печи подтвержден имитационным моделированием системы, что показало работоспособность предложенного алгоритма управления.
ЛИТЕРАТУРА:
- В.Дьяконов. MATLAB 6: УЧЕБНЫЙ КУРС. СПб.: Питер, 2001. – с. 592.
- Хасмамедов Ф. И. Автоматизация управления трубчатыми печами / Ф. И. Хасмамедов. – Москва: Химия, 1980.
- Ягудин М. Н., Абызгильдин Ю. М., Гимаев Р. Н. Теплотехнический расчет трубчатой печи. – Уфа. УГНТУ, 1979. – с. 66.
- Брондз Б. И., Соловьев A. M. и др. Пути повышения эффективности работы печей блоков установок АВТ. Тематический обзор. – М.: ЦНИИТЭнефтехим, 1982. – с. 52.


