Анализ эффективности работы самостабилизатора давления от воздействия гидроудара в системе
К. А. МЯГКОВ – инженер-расчетчик 1 категории ООО «ТехПромАрма»
Н. В. ТАННЕНБЕРГ – инженер-конструктор 2 категории ООО «ТехПромАрма»
В. А ПЕСТУНОВ – генеральный директор ООО «ТехПромАрма»
Р. Ф. ГАФФАНОВ – к.т.н., ООО «Инженерно-расчетная компания «Проект»
Д. Ю. СЕРИКОВ – к.т.н., доцент РГУ нефти и газа имени И. М. Губкина
В статье промоделировано возникновение и распространение гидравлического удара, изучены его влияния и негативные эффекты на трубопроводную систему, авторами предложен и показан принцип работы и эффективность устройства самостабилизатора в устранении негативных эффектов от гидравлического удара.
Трубопроводные системы нефтедобывающих предприятий, атомной энергетики, ЖКХ, химической промышленности и др. являются зонами повышенного внимания и требований к прочности и безопасности. Основным динамическим воздействием, приводящим к разрушению трубопроводной системы установленного на него оборудования, является – гидравлический удар, основные причины возникновения гидравлического удара рассмотрены в работе [1] и являются:
- внезапная остановка насоса или его поломка;
- неконтролируемое срабатывание запорной арматуры;
- переходные режимы (включение и выключение насосов, одновременно работающих в системе).
Гидравлический удар – это скачок давления, возникающий вследствие резкой остановки потока или быстрого изменения скорости течения. Гидравлический удар является причиной динамической нагрузки на трубопровод, арматуру, крепежные элементы, опоры и другие компоненты системы.
В конце 19 века проблему гидравлического удара описал Н. Е. Жуковский, в своих работах он дал объяснение и определение гидравлического удара, предложил методику расчета повышения давления и скорости распространяемой ударной волны [2]. Для описания всех физических эффектов гидравлического удара использовались уравнение движения и уравнение неразрывности. При решении этих уравнений принимались следующие допущения:
- течение жидкости в трубопроводе ламинарное;
- стенки трубопровода абсолютно жесткие;
- течение одномерное.
Результатом преобразований уравнений и принятых допущений была получена формула:
![]()
где:
ρ – плотность протекающей среды;
c – скорость распространения ударной волны (скорость звука) в данной среде;
ν – скорость потока среды (до закрытия запорного органа);
ΔΡуд – максимальное повышение давления при гидравлическом ударе.
Н. Е. Жуковский в своем труде [2] описывает способы и методы нахождения скорости распространения ударной волны, подтвержденные результатами экспериментов, которые отражены в работе [6]. Выведенное им уравнение скорости распространения ударной волны имеет вид:

где:
β –коэффициент сжимаемости среды;
r – внутренний радиус трубы;
δ – толщина стенки трубы;
Е – модуль упругости материала трубы.
Для случая с абсолютно жестким материалом трубопровода:
![]()
Гидравлический удар может привести к разрушению трубопровода. Что, в свою очередь, ведет к утечке среды, биологическому заражению почвы, потере напора, потере прибыли, дополнительным затратам на замену оборудования, трубопровода и восстановление окружающей среды.
Для предотвращения подобных аварий предложено большое количество конструкторских решений и методов, однако, в большинстве своем, конструкции либо требуют дополнительного места в помещениях, либо не воспринимают ударно-волновой процесс (например, сбросной клапан), либо требуют дополнительных источников электроэнергии, которые не всегда возможно обеспечить. Авторами статьи предложен новый способ и абсолютно новая запатентованная конструкция, не требующая дополнительных источников энергии, позволяющая гасить критическое давление гидравлического удара за счет эффекта самостабилизации давления. Запатентованная конструкция показала свою эффективность и является наиболее универсальным, малогабаритным и наименее затратным способом предотвращения негативного влияния гидравлических ударов.
В основу принципа работы самостабилизации были положены следующие диссипативные эффекты гашения:
- рассеивание волны гидравлического удара с использованием группы отверстий;
- изменение геометрии проточной части, создающее контролируемое изменение объема;
- остаточное гашение волн давления в демпфирующих камерах за счет податливости поршня и сжимаемости самой среды.
Для определения эффективности гашения гидравлического удара самостабилизатором давления был проведен вычислительный эксперимент, в плане гидродинамических расчетов, натурно подтвержденных на стенде АО «НИЦ АЭС» в городе Кашира и на опытно-промышленных испытаниях в ПАО «Лукойл».
Для гидродинамического анализа трубопровода и самостабилизатора давления использовался программный код, основанный на численном решении дифференциальных уравнений в частных производных, описывающих поведение потока жидкости и акустические эффекты в сжимаемых и не сжимаемых средах.
В статье представлены результаты моделирования и распространения волны гидравлического удара в трубопроводе с установленным на нем самостабилизатором давления номинальным диаметров DN10, для определения изменения давления в сечениях до и после установленного самостабилизатора.
В расчете использована модель самостабилизатора давления ССД.А.Т.010 по техническим условиям [4]. Условный диаметр – 10 мм. Общий вид самостабилизатора давления представлен на рисунке (рис. 1).
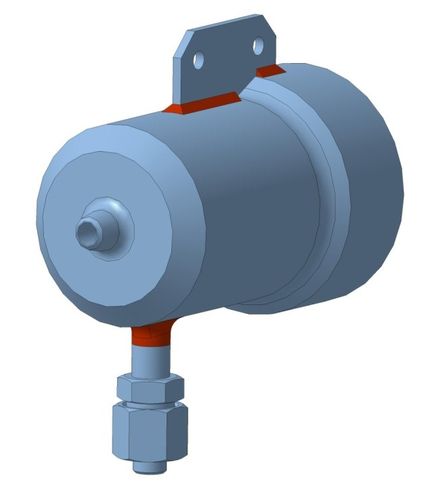
Рис. 1. Общий вид самостабилизатора давления DN10
В расчете приняты следующие условия и допущения:
- расчетная область (рис. 2) представляет собой угловой сегмент в 90° проточной части самостабилизатора давления с примыкающими к ней проточными частями трубопровода. Такое допущение справедливо, при использовании осевой симметрии, при этом программный код согласует между собой результаты решения уравнений в ячейках, находящихся на одной и на другой плоскостях симметрии;
- во избежание влияния границ расчетной области, длина каждой примыкающей части составила 100 мм;
- из описания диссипативных эффектов гашения, была учтена подвижность каждого поршня как свободное движение с одной степенью свободы (в продольном направлении);
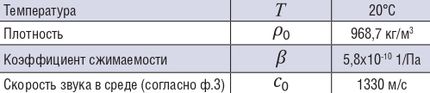
- в качестве материала среды принималась вода 20°С. Начальные параметры среды представлены в таблице (табл. 1);
- материал трубопровода принимался как абсолютно жесткий, что соответствует наиболее опасному расчетному случаю (максимальному повышению давления для заданных параметров), то есть при расчете величины скорости звука c0 в среде используется формула (3);
- начальное давление (абсолютное) p0 в системе выбиралось из условия верхней границы давления гидроиспытаний для самостабилизатора, как соответствующее наиболее опасному расчетному случаю, и составило 8 МПа;
- во избежание появления зон отрыва (вакуума) и локальных каверн (Δpуд ≥ p0) в нестационарном расчете, скорость потока на входе в расчетную область принималась 5 м/с;
- для корректного описания появления гидравлического удара в расчетной области (в данном случае, за счет резкого закрытия запорного органа), помимо учета сжимаемости среды, необходимо описать зависимость изменения плотности от изменения давления.
Таким образом, для описания поведения жидкости было использовано уравнение состояния Тейта [5], связывающее плотность жидкости с давлением:


Рис. 2. Расчетная область
Таблица 1. Параметры рабочей среды
В настройках конечно-элементного разбиения были выбраны следующие параметры:
- характерная форма элементов – гексаэдр;
- характерный размер элемента – 0,5 мм;
- число призматических слоев – 1;
- толщина призматического слоя – 0,1 мм.
Таким образом, сгенерированная конечно-элементная сетка имела размерность 410600 элементов и 464600 узлов.
Гидродинамический анализ состоит из двух этапов:
- этап стационарного расчета, результатом которого является установившийся поток жидкости в системе трубопровода с установленным на нем самостабилизатором;
- этап нестационарного расчета, включающий в себя возникновение и распространение гидравлической ударной волны в среде.
Цель стационарного этапа гидродинамического расчета: определить параметры установившегося потока жидкости путем достижения сходимости результатов и стремления графиков давления и скорости к асимптоте.
Граничные условия приведены на рис. 3. Скорость потока на входе в расчетную область составила – 5 м/с. Давление на выходе – начальное абсолютное давление рабочей среды, p0 = 8 МПа.
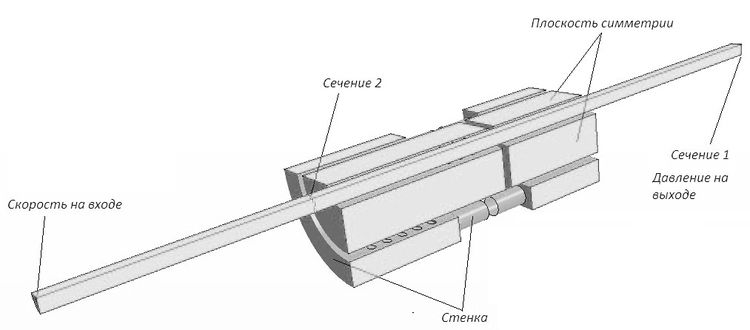
Рис. 3. Граничные условия для стационарного расчета
Сходимость решения оценивалась по целевой функции, в данном случае по скорости в контрольном сечении 1 и по давлению в контрольном сечении 2.
На рис. 4 и 5 показаны график изменения скорости потока и давления от числа итераций соответственно.
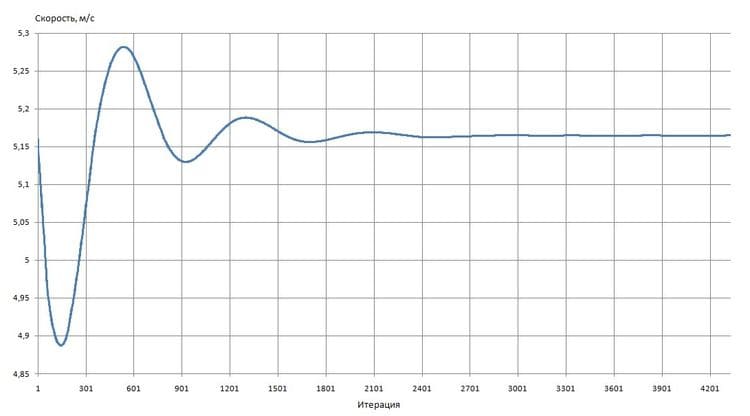
Рис. 4. Зависимость изменения скорости потока в контрольном сечении 1 от числа итераций
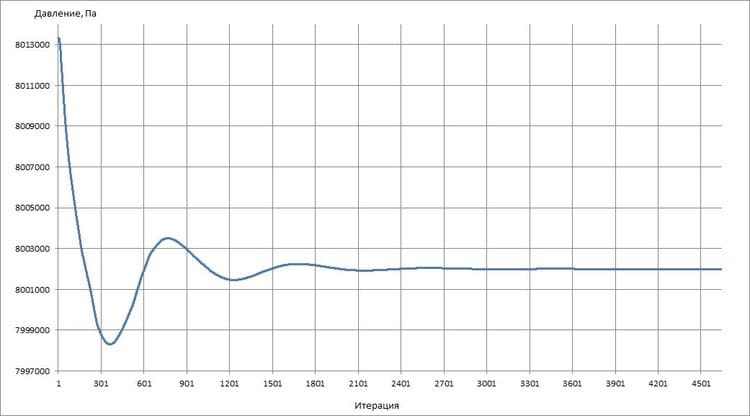
Рис. 5. Зависимость изменения давления в контрольном сечении 2 от числа итераций
Как видно из графиков, после достижения определенного числа итераций решение практически не меняется, что соответствует сходимости решения, при этом значения давления и скорости принимают установившиеся значения:
v = 5,16 м/с;
p = 8,002 МПа.
Все необходимые параметры установившегося течения жидкости для проведения нестационарного расчета были получены.
Цель нестационарного этапа гидродинамического расчета – провести анализ эффективности работы самостабилизатора давления путем определения зависимости изменения амплитуды абсолютного давления в контрольных сечениях (до и после самостабилизатора).
Под контрольными сечениями подразумеваются сечения трубопровода, в которых время динамического воздействия среды на стенки наибольшее (место непосредственного возникновения гидравлического удара; сечение трубопровода, расположенное за самостабилазотором давления, то есть с противоположной стороны от места возникновения гидравлического удара).
Возникновение гидравлического удара моделировалось путем изменения граничного условия «Давление на выходе», использованного в стационарном расчете, на граничное условие «Стенка». Такое изменение граничного условия позволяет воссоздать (смоделировать) поведение жидкости при резком закрытии запорного органа и воспроизвести эффект, возникающий при гидравлическом ударе. Граничные условия для нестационарного расчета представлены на рис. 6.
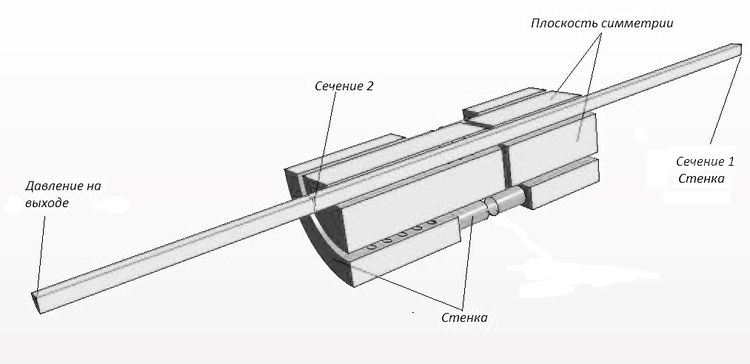
Рис. 6. Граничные условия для нестационарного расчета
Согласно критерию Куранта – Фридрихса – Леви (CFL) [7] минимальный шаг по времени определялся как:

Данное условие было выбрано исходя из заявленного в технических условиях [4] на самостабилизаторы снижения давления до безопасного уровня: не менее чем в 10 раз. Такое снижение давления после самостабилизатора является достаточным для обеспечения прочности и надежности трубопровода и арматуры на всем заявленном сроке службы. Другими словами, нестационарный расчет велся до момента, когда амплитуда колебания абсолютного давления в части трубопровода до самостабилизатора давления будет в 10 раз меньше, чем амплитуда колебания в момент возникновения гидравлического удара (рис. 7).
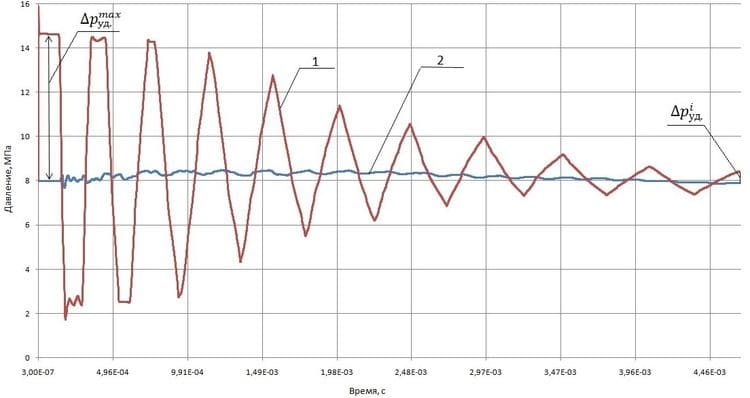
Рис. 7. График изменения абсолютного давления: 1 – в контрольном сечении 1 (место возникновения гидравлического удара) 2 – в контрольном сечении 2 (на выходе из самостабилизатора давления)
Согласно графику 1 на рисунке 7, Δpiуд и Δpmaxуд не превышает 0,48 МПа (при i = 11) и 6,67 МПа соответственно, откуда 0,1 × Δpmaxуд = 6,67 Мпа, условие окончания расчета выполнено.
В качестве оценки корректности постановки задачи использовалось сравнение величин повышения давления Δpуд, рассчитанное по формуле (1), с величиной давления Δpmaxуд, полученной при помощи математического моделирования.
Повышение давление, рассчитанное по формуле (1): Δpуд = 6647994,4 Па.
Повышение давление, полученное при помощи математического моделирования: Δpmaxуд = 6668025,1 Па.
Погрешность составила 0,3%.
Дополнительной проверкой будет сравнение полупериода колебаний давления, рассчитанного аналитическим методом (по формуле 6), и полученного при помощи математического моделирования (рис. 8).
Полупериод колебания – это время, за которое звуковая волна пройдет расстояние равное двум длинам трубопровода до места ближайшего расширения.
Очевидно, зная длину трубопровода Ιтр (100 мм) и скорость звука в среде c0 (1330 м/с), можно определить время, за которое волна пройдет расстояние в 200 мм:

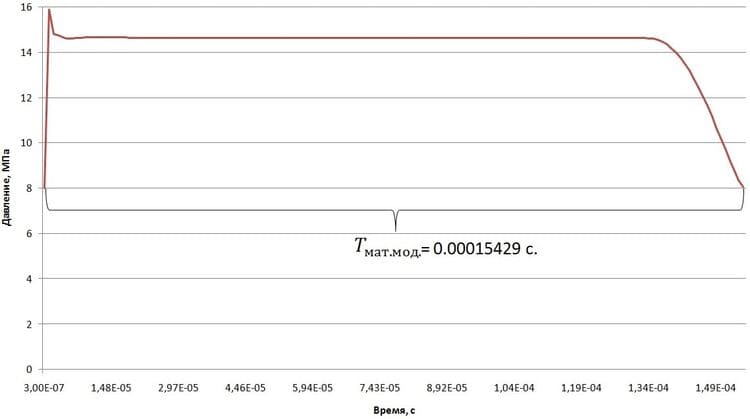
Рис. 8. График первого цикла повышения давления в контрольном сечении 1 (место возникновения гидравлического удара)
Согласно графику на рис. 8, полупериод колебания, полученный при помощи математического моделирования составил: Тмат мод = 0,00015429с.
Погрешность составила 2,5%.
Таким образом, выполненное сопоставление величин подтвердило, что постановка задачи в части физико-математической модели и результаты расчета не содержат противоречий с известной физической картиной и аналогичными решениями [2,3,6].
Графики изменения абсолютного давления, представленные на рис. 7, явно показывают эффективность работы самостабилизатора. Максимальное повышение давления в контрольном сечении 1 за все время расчета составило Δpmaxуд = 6,67 Мпа (до самостабилизатора), соответственно максимальное повышение давления в контрольном сечении 2 за все время расчета Δpссд = 0,48 Мпа (после самостабилизатора). Отсюда, эффективность работы самостабилизатора определяется отношением
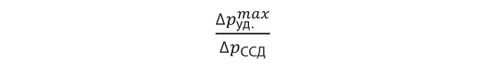
и равно 13,89, другими словами, динамическая нагрузка на трубопроводную систему с установленным на ней самостабилизатором давления снизилась более чем в 13 раз.
Результаты исследований подтверждены экспериментально на стенде АО «НИЦ АЭС» в городе Кашира и на опытно-промышленных испытаниях в ПАО «Лукойл». Данные исследования позволили разработать линейку самостабилизаторов давления и внедрить их в производство.
Дальнейшей целью исследований будет определение влияния гидродинамической нагрузки от среды на стенки трубопровода.
ЛИТЕРАТУРА:
- Гаффанов Р. Ф., Щенятский А. В., Сериков Д. Ю. Анализ проблем расчета запорной арматуры с нанесенным на нее коррозионным покрытием. «Строительство нефтяных и газовых скважин на суше и на море». №7, 2016, ISSN 0023-1126 с. 23–27.
- Жуковский Н. Е. О гидравлическом ударе в водопроводных трубах. – М. – Л., 1949, с. 105; ил.
- Чарный И. А. Неустановившееся движение реальной жидкости в трубах. – М. – Л., 1951, 224с. ил.
- Технические условия ТУ 3790-001-78976334- 2012 «Самостабилизатор давления Технические условия»
- Tait P.G. Report on Jome of the Physical Properties of Water. – 1888. – V. 47
- Ганиев Р. Ф., Низамов Х. Н, Дербуков Е. И. Волновая стабилизация и предупреждение аварий на трубопроводах. – М.: Изд-во МГТУ им. Н. Э. Баумана, 1996. – с. 260.
- R. Courant, K. Friedrichs, H. Lewy Über die partiellen Differenzengleichungen der mathematischen Physik // Mathematische Annalen. – 1928. – Т. 100, № 1. – с. 32–74.


