Один из подходов к математическому моделированию транспорта газа на базе гибридных вычислительных систем
С. В. СПИРИДОНОВ – Институт проблем управления РАН, лаборатория № 19 «Многосвязных систем управления»
Д. Ю. СЕРИКОВ – к.т.н., доцент, кафедра «Стандартизация, сертификация и управление качеством производства нефтегазового оборудования» РГУ нефти и газа имени И. М. Губкина
В статье описывается новый подход к моделированию потоков в сложных газотранспортных системах, с использованием гибридных многопроцессорных вычислительных систем на базе вычислительных кластеров смешанного типа для решения задач оперативного диспетчерского управления (ОДУ) транспортом газа.
Под сложными газотранспортными системами (ГТС) понимается сети газопроводов произвольной конфигурации (с закольцованными подсистемами) предназначенные для магистрального транспорта газа от месторождений к промышленным и административным центрам, включая экспорт газа в другие страны, газораспределительные сети и т.д. Отдельные ветви газопроводов – это одна или несколько параллельных ветвей трубопроводов (нитки), соединенные между собой перемычками (лупингами и т.д.). Вдоль ветвей магистральных газопроводов могут быть расположены промежуточные компрессорные станции (КС), а также промежуточные отборы (стоки) для крупных потребителей (ГРЭС, ТЭС и др.) и притоки от источников, т.е. месторождений и подземных хранилищ газа (ПХГ) (рис. 1).
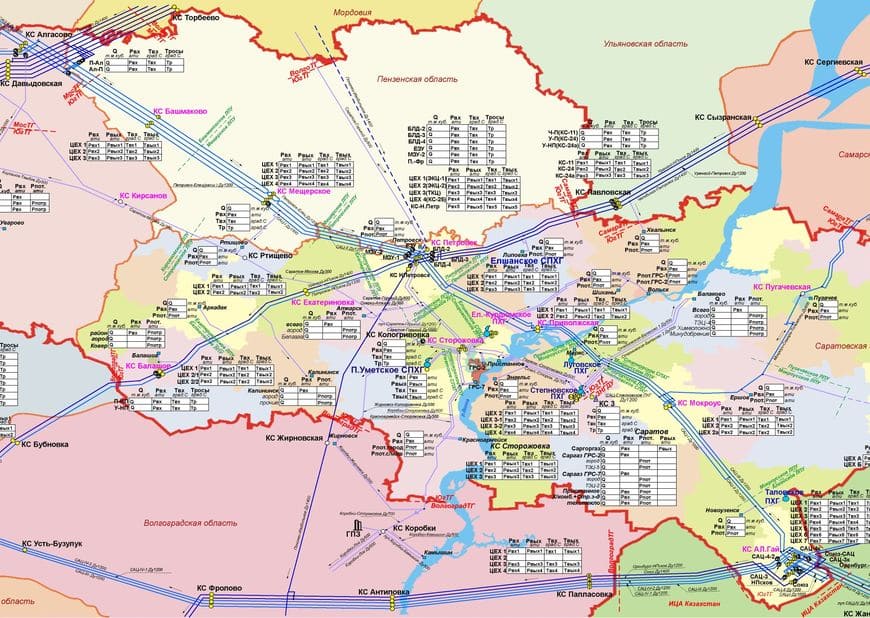
Рис. 1. Сложная газотранспортная система
ГТС объединяются в крупнейшую в мире единую систему газоснабжения (ЕСГ) России. ЕСГ характеризующаяся многокомпонентность, сложностью протекания процессов и управления подразумевает использование системного подхода. Только системных подход способен обеспечить высокое качество управления такими задачами как: оптимальное маневрирование потоками газа; иерархическая организация контроля; диспетчерское управление в реальном времени; ОДУ режимами работы объектов системы и т.д. [2]
Важнейшей частью управления ЕСГ является решение режимно-технологических задач в рамках ОДУ и вопросах планирования. Сложность ОДУ характеризуется следующими особенностями: большая размерность ГТС; непрерывность процессов; нелинейность протекания процессов; сложностью организации ГТС; отсутствие достаточного количества средств телемеханики и д.р.
Для решения задач ОДУ в настоящее время применяются средства моделирования на базе регламентированных расчетных схем, которые являются сильно упрощенными моделями реальных объектов [5]. Соответственно, одним из способов повышения качества ОДУ является применение адекватных средств моделирования, максимально приближенных к реальному объекту, что предъявляет соответствующие требования не только к самой модели, но и к ее реализации на соответствующей программно-аппаратной платформе (ПАП).
Классический подход к моделированию ГТС
В общем случае, на основании закона сохранения массы, количества движения и энергии, для произвольного объема жидкости V, ограниченного замкнутой поверхностью S можно записать в интегральной форме [3,6]
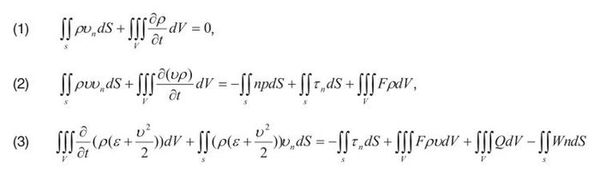
где:
p – давление,
ρ – плотность,
υ – скорость газа в данной точке,
υN – проекция на внешнюю нормаль n к поверхности S,
ΤN – напряжение трения на площадке с внешней нормалью n,
F – напряжение массовой силы,
Q – удельная мощность источников тепла,
W – вектор плотности потока тепла,
ε – удельная внутренняя энергия газа.
Под классическим подходом понимается использование модели движения сжимаемого газа в случае длинного трубопровода, где его длина существенно больше диаметра поперечного сечения и пренебрежением изменения скоростного напора по длине, что позволяет свести задачу к эквивалентной одномерной [3].
Для практических расчетов исходная система уравнений упрощается посредством предположения изотермичности (T = const) и стационарности процесса, дозвуковой скорости течения газа (отсутствие волнового члена), отсутствия больших перепадов высот (до 500 м), постоянности сечения длинного трубопровода и линеаризации
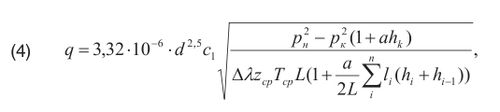
где:
a = ∆/(14,64TcpZ), значение коэффициента c1 принимается в зависимости от системы измерений (СИ или смешанной системы),
∆ – относительная плотность газа по воздуху,
pH – давление в начале участка,
pK – давление в конце участка,
Tcp – средняя по длине участка газопровода температура транспортируемого газа,
Zcp – средний по длине газопровода коэффициент сжимаемости газа,
λ – коэффициент гидравлического сопротивления,
L – длина участка газопровода,
hк – превышение или снижение конечной точки расчетного участка относительно начальной точки,
hi – превышение или снижение i-ой точки трассы относительно начальной точки,
li – длина i-го элемента участка газопровода.
Коэффициент гидравлического сопротивления — это функционально зависимая величина от числа Рейнольдса Re и относительной шероховатости трубы δ - λ = f (Re, δ). Давление в начале участка вычисляется как разность между давлением на выходе компрессорного цеха (КЦ) и суммой потерь давления в системе охлаждения с потерями давления между КЦ и узлом подключения к линейной части. Расчет остальных параметров так же описан в нормативе [5].
Современный подход с использованием МВС
Наличие различных критериев и уход в сторону решения систем нелинейных уравнений предполагает комплексный подход к получению конечного результата, учитывающий все аспекты программо-аппаратной платформы (ПАП) моделирования. Программная составляющая ПАП включает в себя численные методы, позволяющие построить устойчивые вычислительные алгоритмы, средства ввода, вывода и представления информации. Аппаратная часть должна соответствовать требованиям программной (хотя возможно и обратное отношение). Таким образом, задачей комплекса ПАП является решение поставленной задачи за отведенное время.
Для решения различных прикладных газодинамических задач применяется множество методов, таких как методы конечных разностей, конечных объемов, конечных элементов. Наиболее часто используемым численным методом является метод конечных. Разработанные разностные схемы имеют хорошую точность и устойчивость, однако при больших размерностях ГТС для эффективного решения требуется специальная ПАП, в противном случае время решения будет слишком большим.
В роли ПАП, удовлетворяющей всем предъявленным требованиям, в настоящее время выступает направление кластерных вычислений, с развитием которой сильно возрастает роль численных методов. В результате появились многопроцессорные высокопроизводительные вычислительные системы (МВС), способные решать задачи большой размерности за приемлемое (или существенно меньшее) время в отличие от традиционного подхода за счет параллельного расчета. Существует различные типы МВС как по структуре организации, так и по способам организации вычислений. В настоящее время наиболее часто встречаются представители кластерных МВС – объединенные высокоскоростной сетевой инфраструктурой многопроцессорные системы, главным образом решающие задачи большой размерности. Стремительно развиваются МВС на базе графических ускорителей (например, NVIDIA Tesla) или FPGA, что позволяет эффективно проводить моделирование отдельных частей ТГС, таких как ГПА и т.п. Программная составляющая подобных систем представлена многообразием языков программирования и библиотек (fortran, CC++, OpenCL, MPI, CUDA и т.д.). Однако, для эффективного использования МВС необходима советующая («параллельная») реализация вычислительного метода, что не всегда возможно. Для сетевых и других задач такие методы существуют, что существенно экономит время и повышает точность при решении поставленных задач. Таким образом, наиболее перспективным направлением в решении режимно-технологических задач ОДУ является использование ПАП на базе МВС.
Рассмотрим один из способов решения задачи ОДУ в случае нестационарности реального газа с использованием МВС [1,4]. Нестационарный изотермический режим с учетом упрощений и линеаризации квадратичного члена сведем к уравнению теплопроводности:

с начально-краевыми условиями (одним из трех):
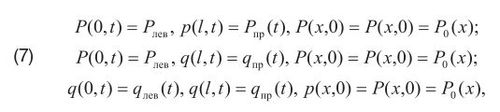
где: P0(x) – распределение давления вдоль участка в начальный момент времени t = 0,Pлев(t),
Pпр(t), qлев(t), qпр(t) – заданные функции изменения давления и расхода на границах участка в рассматриваемом интервале времени [0,T], ù = (u21 + u1u0 - 2u20)/u1 - u0, где: ù – средняя скорость, uo – скорость в начале и конце (u1) участка.
Для решения различных прикладных газодинамических задач применяется множество методов, таких как методы конечных разностей, конечных объемов, конечных элементов. Разработанные разностные схемы имеют хорошую точность и устойчивость, однако при больших размерностях ГТС для эффективного решения требуется специальная ПАП, в противном случае время решения будет слишком большим.
Переписав уравнения в дивергентной форме можно воспользоваться аппроксимацией по различным схемам (например, по явной)
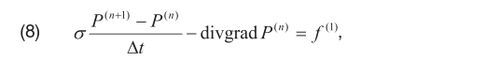
где:
ƒ – функция распределения источников.
Конечно-объемная аппроксимация по явной схеме
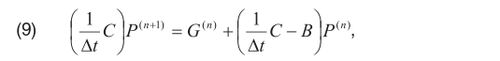
где матрица B (матрица жесткости) есть аппроксимация члена -divgradP, матрица C (матрица массы) – аппроксимация σ·ðp/ðt.
Далее формируется СЛАУ в виде AP = F, где A = B + C/∆t, F = G1 + ∆t -1CP(0), P(0) = (P0(x1),…,P0(xk))T, которая может быть решена, например, с помощью метода верхней релаксации [1,4].
Данный подход может быть использован и для расчета на GPU, но с учетом существенного ограничения под размерности задачи не целесообразен.
С другой стороны, расчет на GPU, вполне применим для эффективного решения частного случая в составе ГТС, причем, возможен расчет не только линейных участков, но и, например, режим работы ГПА. В результате снимается лишняя нагрузка на CPU, однако это требует соответствующей реализации необходимых алгоритмов.
Подход с использованием гибридных МВС
Каждый вид МВС по отдельности достаточно освоен и применяется для соответствующих специфических, для каждого типа, задач. Однако следующим логичным шагом должно быть объединение подобных систем в многопроцессорную систему гибридного типа (МСГТ). Конфигурация МСГТ, с точки зрения технической реализации, может быть разной, но большей части узко специализированной под конкретные задачи, в противном случае она может оказаться слишком избыточной, особенно в части сетевого взаимодействия и с внешней памятью.
В МСГТ можно выделить четыре основных компоненты: многопроцессорные системы на базе CPU; межсистемное взаимодействие посредством организации высокопроизводительной сети; межсистемной взаимодействие для доступа к оперативной памяти; вычислительной системы на базе GPU.
Обычно, многопроцессорные системы на базе CPU объединяются в кластер путем организации высокопроизводительной сети (например, infiniband), что позволяет производить обмен данными между узлами.
Проблема возникает при доступе к системной памяти из GPU, поэтому в данном случае используется собственная память, что позволяет эффективно проводить вычисления, но если необходимо обращаться к системной памяти, то производительность существенно снижается. Соответственно, в случае обмена информацией с других узлов, общая производительность будет ограничена работой межсетевого взаимодействия. Однако в настоящее время ведутся работы по снижению издержек доступа к системной памяти (например, NVidia NVLINK) увеличивающие скорость доступа в несколько раз.
Таким образом, единственным способом использовать подобный подход заключается в декомпозиции задачи и соответствующей реализации вычислительной процедуры.
Отдельно стоит выделить проблему балансирования нагрузки на CPU/GPU, что вытекает из-за разницы в аппаратном обеспечении для доступа к памяти.
Задача декомпозиции ГТС заключается в выделении относительно небольших объектов с минимальным обменом информацией с системной памятью для расчетов на GPU. Т.е. с точки зрения уровня CPU (глобального) стоит задача постановки начально-краевых условий для нижнего уровня.
Затем на глобальном уровне происходит окончательное решение системы уравнений.
ВЫВОДЫ
- Эволюционно решение задач ОДУ прошло путь от использования наиболее упрощенных моделей вследствие отсутствия доступных математических методов решения и неразвитостью первых вычислительных систем до богатства современных моделей в области учета и динамичности включаемых факторов, позволяющих существенно приблизиться к реальному объекту управления, многообразия математических методов решения и готовности современных вычислительных систем.
- Логичным объединением современных технологий является ВСГТ, позволяющая использовать лучшие стороны МВС на базе CPU и GPU – решение задач большой размерности и быстрота (высокая точность) расчета отдельных компонент модели.
- К минусам такого подхода можно отнести относительно узкую специализированность конфигурации, необходимость в аккуратности реализации алгоритма с учетом принципиальной возможности его реализации. С другой стороны, использование МСГТ открывает новые направления в области алгоритмизации и параллельных вычислений, что в перспективе позволит создать ПАП для более эффективного решения задач ОДУ.
ЛИТЕРАТУРА:
- Ахметзянов А. В., Сальников А. М., Спиридонов С. В. Многосеточные балансовые модели нестационарных потоков в сложных газотранспортных системах // Управление большими системами. 2010. № 30.1. с. 230–251.
- Панкратов В. С., Ажикин В. А., Степанян А. А. АСДУ транспортом газа / издательство: ЗАО «Экон-информ», 2014 г., твердый переплет – 661 стр., ISBN 978-5-9506-1185-8
- Селезнев В. Е., Алешин В. В., Клишин Г. С. Методы и технологии численного моделирования газопроводных систем. М.: Едиториал УРСС, 2002. – с. 448 – ISBN 5-354-00249-4.
- Спиридонов С. В. Параллельные алгоритмы при моделировании стационарных процессов в ГТС / Труды 8-й Всероссийской школы-конференции молодых ученых «Управление большими системами» (УБС’2011, Магнитогорск). Магнитогорск: Магнитогорского государственного технического университета им. Г.И. Носова, 2011. с. 289–293.
- СТО Газпром 2-3.5-051-2006г. 6.Чарный И. А. Неустановившееся движение реальной жидкости в трубах. М.: Недра, 1975. – с. 296.


