Методика проектирования геометрии вооружения шарошечного бурового инструмента на основе математического моделирования
С. В. СПИРИДОНОВ – Институт проблем управления РАН
Д. Ю. СЕРИКОВ – к.т.н., доцент РГУ нефти и газа имени И. М. Губкина
Разработана методика проектирования геометрии вооружения шарошечного бурового инструмента на основе математического моделирования процесса его износа на базе методов планирования и организации эксперимента. Предложенная методика позволяет за счет возможности фиксации величины одного из основных параметров бурения (например, нагрузки на долото), с достаточной точностью определить рекомендуемый угол заострения и шаг зубьев, обеспечивающих максимальную эффективность работы вооружения на всех основных типах, разбуриваемых горных пород.
Конструирование вооружения шарошечного бурового инструмента, как правило, основано на предположении, что зубья шарошек внедряются в породу на ту или иную глубину, в зависимости от крепости разбуриваемых пород. Однако, такое предположение верно только при бурении мягких и средних пород, обладающих небольшой твердостью. При бурении крепких пород, даже при максимально допустимых нагрузках на долото, зубья шарошек зачастую не внедряются в поверхность забоя. В этом случае разрушение породы носит объемноусталостный характер и лишь в незначительной степени происходит поверхностное разрушение. Доказательством этого может служить тот факт, что при разбуривании крепких пород выносимый на поверхность шлам содержит значительный процент крупных частиц, которые никак не могут образоваться при поверхностном разрушении горных пород.
Очевидно, при разбуривании крепких пород влияние фактора времени контакта зуба шарошки с породой становится менее значительным, особенно для хрупких пород, чем при разбуривании пород, обладающих значительной пластичностью. Эффективность разрушения таких пород особенно возрастет при высокой частоте ударов по одному и тому же месту. По мере повышения контактного давления число ударов, необходимое для объемно-усталостного разрушения, понижается, и, наконец, при некоторой силе удара разрушение наступает после первого же удара по всей напряженной зоне [1].
Многочисленными теоретическими и лабораторными исследованиями установлено, что разрушение горных пород при бурении шарошечными долотами носит скачкообразный характер. Разрушение протекает следующим образом: в течение некоторого времени создается напряженное состояние в породе, а затем, когда напряжение достигает предела прочности, наступает разрушение. Эйгелес Р. М. математическим путем получил формулу для определения минимального времени контакта зубьев долота с породой, которое необходимо для создания напряженного состояния и начала хрупкого разрушения [1]:

При этом необходимо стремиться к тому, чтобы время воздействия зубьев вооружения шарошек на забой удовлетворяло условию:
![]()
В этом случае скорость бурения будет стремиться к своему максимуму, а удельный износ инструмента и удельный расход энергии к минимуму. Время контакта зуба вооружения с породой можно определить по следующей формуле [1]:


При ограниченной нагрузке на долото величину контактного давления можно увеличить путем уменьшения числа зубьев, что во многих случаях позволит перейти к более эффективному объемному разрушению. Уменьшение числа зубьев приводит к пропорциональному, увеличению времени контакта каждого зуба с забоем и одновременно уменьшает минимально необходимое время за счет увеличения скорости встречи зуба с породой.
С уменьшением количества зубьев вооружения шарошек, разрушение породы приобретает ударный характер. При этом увеличивается зазор между телом шарошки и поверхностью забоя, что существенно улучшает условия выноса шлама из-под зубчатых элементов шарошек бурового инструмента.
Данные, полученные на практике, полностью подтверждают сказанное. Так, было установлено, что при бурении песчаников средней крепости долота, предназначенные для бурения мягких пород, дают большую механическую скорость и проходку на долото по сравнению с долотами, предназначенными для бурения средних пород, при одинаковых режимах бурения.
Одной из важных компонент в задаче повышения эффективности вооружения шарошечного бурового инструмента, является изучение изменения его работоспособности под воздействием различных факторов. На основании этих данных можно выявить наиболее важные факторы, влияющие на эффективность работы вооружения шарошечного бурового инструмента, при учете возможности влияния межфакторного взаимодействия. Обладая подобными данными, удастся не только лучше понять природу взаимодействия зубьев вооружения с разбуриваемой породой, а также их износа, но и осуществить математическое моделирование этих процессов. С другой стороны, подобные исследования должны отвечать различным требованиям, чтобы в итоге положительно сказаться на качестве конечной модели объекта. В настоящее время для решения таких задач широко используются методы планирования и организации эксперимента. Данный математический аппарат позволяет успешно решать множество практических задач в сфере нефтегазовой отрасли, начиная от разработки конкретных деталей машин и механизмов и заканчивая определением различных физических параметров нефтегазотранспортных систем.
Задача заключается в идентификации основных факторов, наиболее влияющих на эффективность работы бурового инструмента. Основными ограничениями, как правило, является износ не более трети высоты вооружения за определенный промежуток времени и критическое увеличение площади площадки притупления. Это связано с тем, что именно величины вылета и размеры площадки притупления характеризуют работоспособность вооружения породоразрушаюшего инструмента и определяют его ресурс работы. Уменьшение вылета и соответствующее увеличение площади площадки притупления зубьев вооружения в процессе бурения приводит к значительному снижению единичной ударной нагрузки зуба о забой, падению удельного контактного давления зубьев на породу и как следствие снижению технико-экономических показателей бурения [2].
Под планированием эксперимента в данном случае понимается составление факторного плана ПФЭ (полный факторный эксперимент), который учитывает независимые факторы (между ними должна отсутствовать корреляция), их взаимосвязь, порядок и количество испытаний [5].
Результатом спланированного и проведенного эксперимента является исследование отклика системы (параметра оптимизации) в различных формах с соответствующими выводами об объекте исследований с заданной точностью. Необходимо получить адекватную модель на выбранной подобласти факторного пространства, значение отклика которое не должно отличаться от фактического значения более чем на некоторую заданную величину. Таким образом, в данном случае решается задача построения регрессионной модели.
Модель объекта представляется в виде черного ящика (рис.1), где Χ1...ΧΚ – факторы, действующие на объект, γ – отклик системы, ƒ – функция отклика.
По результатам однофакторных экспериментов, проведенных на установке и на основе методики ОАО НПО «Буровая техника» – ВНИИБТ выявлено, что на работу вооружения в определенных условиях бурения в основном оказывают три фактора [3]:
- Ф1 – угол заострения зубьев вооружения, определяющий интенсивность изменения площади площадки притупления зубьев в процессе износа вооружения;
- Ф2 – величина вертикальной нагрузки на зуб вооружения;
- Ф3 – угол встречи зубьев вооружения с поверхностью забоя, определяющий шаг и вылет зубьев.
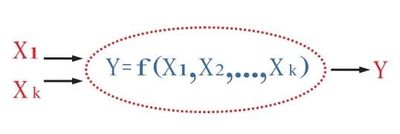
Рис. 1. Модель объекта исследования
Таким образом, зная общее число факторов, можно вычислить максимальное количество экспериментов:

Составим матрицу планирования эксперимента 23 (таблица 1) соблюдая следующие обозначения: если фактор находится на верхнем уровне (максимальное значение), то ставится буква, если все факторы на нижнем уровне, то устанавливается условие (5). Кодирование значений таблицы (+1; –1) выполняется с помощью линейных преобразований координат факторного пространства с центром начала координат в нулевой точке:

Таблица 1
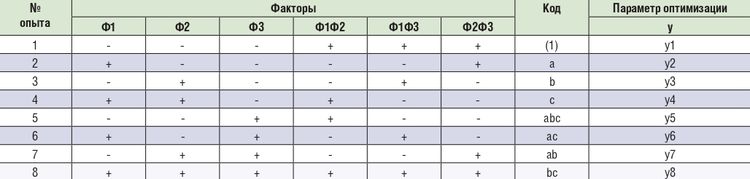
Полученная матрица планирования должна соответствовать таким требованиям ортогональности, симметричности, условиям нормировки.
Математическая модель эксперимента без учета коэффициентов тройного взаимодействия (второго уровня) примет вид линейного полинома первой степени с учетом предположения о линейности процесса:


Для проверки адекватности математической модели использовался критерий Фишера и результаты проверки подтвердили ее адекватность (коэффициенты указаны в таблице 4).
Как отмечалось ранее, с целью экспериментального определения влияния величин: угла заострения зубьев, величины вертикальной нагрузки и угла встречи зуба с забоем, на стойкость вооружения бурового инструмента к знакопеременным динамическим нагрузкам, были проведены испытания ударно-абразивной стойкости поверхностно-армированного зубчатого вооружения.
Испытания проводились на установке и на основе методики – ВНИИБТ [2,3]. Сущность методики заключается в следующем. Изготавливаются образцы породоразрушающих элементов по форме элементов вооружения бурового инструмента в виде зубков диаметром 20 мм. Образец вооружения закрепляется в специальной зажимной обойме, находящейся в нижней части штока, совершающего возвратно-поступательное движение.
Движение штока вверх осуществляется при помощи кулачкового механизма, а движение вниз осуществляется под действием собственного веса и веса навесных грузов. В процессе работы установки, образец вооружения совершает возвратно-поступательное движение в вертикальной плоскости. В нижней точке этого движения происходит соударение зубка с наклонным забоем, закрепленным в наковальне. Удар зубка о наклонный забой осуществляется в присутствии абразива. Регулирование энергией удара зубка о забой может осуществляться двумя способами, либо изменением количества навесных грузов, либо количества регулировочных пластин.
В процессе работы установки через каждые 2000 циклов нагружения производится поворот наклонного забоя на 180° и замена абразива с одновременным замером износа вооружения. Испытания проводились с различными величинами энергий удара, углами наклона забоя и углами заострения зубчатых элементов, соответствующими условиям работы бурового инструмента при бурении пород различных категорий твердости. Основные параметры испытаний приведены в таблице 2.
Таблица 2
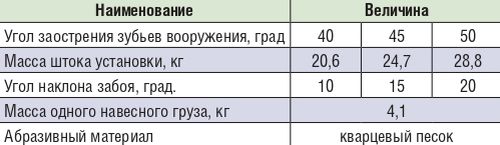
Таблица 3

Таблица 4
![]()
Результаты практических испытаний y и математического моделирования y* представлены на рис. 2, и в таблице 3. В таблице 4 представлены рассчитанные коэффициенты регрессии bj модели (8). Зависимость между наблюдаемыми и предсказанными значениями показана на рис. 3. Предсказанные средние значения для y* представлены на рис. 4.
Проведенные в работе теоретические исследования хорошо согласуются с полученными экспериментальными данными. В результате спланированного и проведенного эксперимента получена адекватная математическая модель износа зубчатых элементов вооружения. Установлена степень влияния, как одиночных факторов, так и их межфакторного взаимодействия.
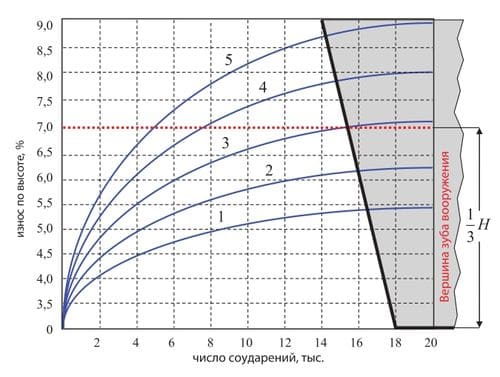
Рис. 2. Зависимость износа зубьев по высоте от нагрузки: 1. При весе грузов 26,0 кг; 2. При весе грузов 28,0 кг; 3. При весе грузов 30,0 кг; 4. При весе грузов 32,0 кг; 5. При весе грузов 34,0 кг.
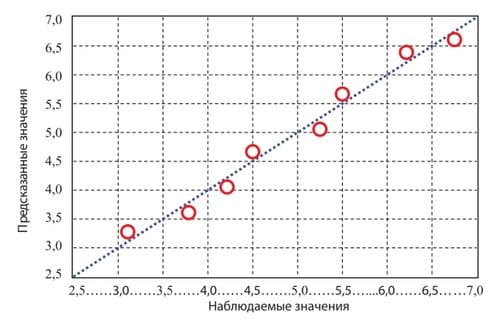
Рис. 3. Зависимость между наблюдаемыми и предсказанными значениями
Из анализа математической модели по основным факторам следует, что наиболее сильное влияние на износ вооружения оказывает величина вертикальной нагрузки на зуб вооружения. Угол заострения вооружения и угол наклона поверхности забоя являются менее значимыми факторами. Так же, необходимо отметить, что полученные коэффициенты отражают влияние факторов только в локальной области факторного пространства.
На основе математического моделирования процесса износа зубчатого вооружения под воздействием различных факторов была разработана методика, позволяющая на стадии проектирования бурового инструмента определять геометрические параметры зубьев его вооружения.
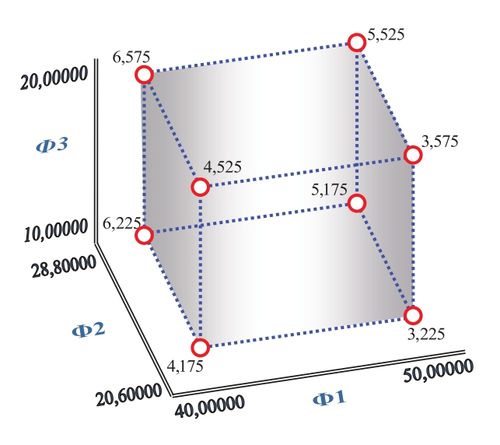
Рис. 4. Предсказанные средние значения для y*
Суть ее заключается в следующем. Фиксируя один из основных параметров на основании зависимости y* от различных факторов Ф1, Ф2 и Ф3 (рис. 5, рис. 6), полученной в результате математического моделирования, можно решать как прямую – определение износа в рамках подобласти факторного пространства, так и обратную задачу – определение значений факторов в зависимости от износа.
Например, если зафиксировать вертикальную нагрузку на зуб вооружения, можно определить угол заострения и шаг зубьев, обеспечивающих максимальную эффективность работы вооружения в данных условиях бурения (рис. 5).
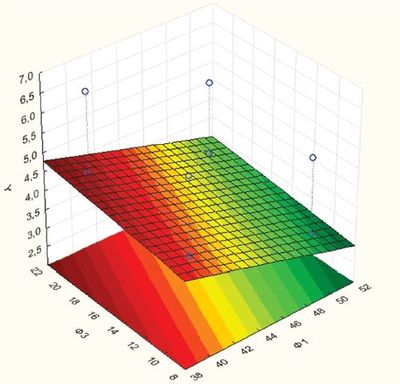
Рис. 5. Карта зависимости Y* от различных факторов Ф1, Ф3 и фиксированном Ф2
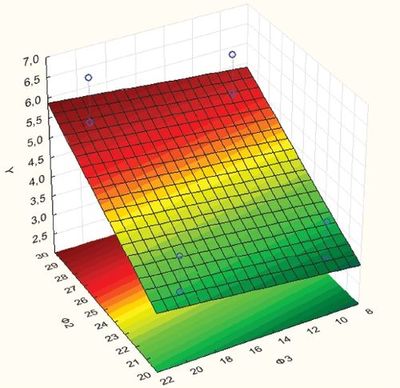
Рис. 6. Карта зависимости Y* от различных факторов Ф2, Ф3 и фиксированном Ф1
При фиксации одной из геометрических характеристик, т.е. шага или угла заострения зубьев и по ним определяется предпочтительное значение вертикальной нагрузка на элементы зубчатого вооружения (рис. 6).
В более общем случае, необходимо провести дополнительные исследования для описания почти стационарной области, т.е. определить ее границы и форму, что позволит применять более гибкие критерии при решении поставленных задач [2].
Предложенная методика позволяет существенно упростить задачу проектирования геометрии зубчатого вооружения шарошечного бурового инструмента. За счет возможности фиксации величины одного из основных параметром бурения (например, нагрузки на долото), можно с достаточной точностью определить рекомендуемый угол заострения и шаг зубьев, обеспечивающих максимальную эффективность работы вооружения на всех основных типах, разбуриваемых горных пород.
Таким образом, использование данной методики при проектировании геометрии различных типов вооружения, позволит значительно снизить время и финансовые затраты на создание новых конструкций шарошечного бурового инструмента.
ЛИТЕРАТУРА:
- Варламов П. С. О механизме разрушения горных пород трехшарошечным долотом. – Нефтяное хозяйство, №8, 1961.
- Сериков Д. Ю. Повышение эффективности шарошечного бурового инструмента с косозубым вооружением. – М.: Нефть и газ, 2015.
- Сериков Д. Ю. Разработка конструкции и технологии изготовления бурового инструмента для РТБ с центробежно-объемно-армированным вооружением. Кандидатская диссертация. М., 1992.
- Сидняев Н. И. Теория планирования эксперимента и анализ статистических данных. Учебное пособие для магистров. Издание 2. М: Издательство «Юрайт», 2014.
- Адлер Ю. П., Маркова Е. В., Грановский Ю. В. Планирование эксперимента при поиске оптимальных условий. – М.: Наука, 1976.


