Совершенствование методики расчета резьбовых фланцевых и межфланцевых соединений
К. А. МЯГКОВ – инженер ООО «Инженерно-расчетная компания «Проект»
Р. Ф. ГАФФАНОВ – к.т.н., ООО «Инженерно-расчетная компания «Проект»
Д. Ю. СЕРИКОВ – к.т.н., доцент РГУ нефти и газа имени И. М. Губкина
В данной статье рассмотрены существующие методики расчета фланцевого соединения, определены факторы, влияющие на напряженно-деформированное состояние деталей, входящих во фланцевое соединение и не учтенные в существующих методиках расчета. Показан вид компоновки существующих методик и виды компоновок с неучтенными факторами воздействия. Описана структура усовершенствования методик прочностного расчета. Обоснована применимость метода конечных элементов при исследовании фланцевых соединений.
Трубопроводная арматура является неотъемлемой частью всех трубопроводных систем, начиная от жилищно-коммунального хозяйства и заканчивая системами с повышенными требованиями к технической безопасности, к которым относятся:
- системы нефтедобывающих и нефтеперерабатывающих предприятий;
- системы водоснабжения тепловых электростанций;
- основные контуры атомной электростанции;
- системы в химическом производстве и переработка.
В данных отраслях промышленности предъявляются повышенные требования к прочности и надежности всех элементов арматуры, а в особенности фланцевых и резьбовых соединений. Фланец – основной элемент соединения трубопроводных конструкций, который обеспечивает прочное и плотное разъемное соединение. Требования к прочности, надежности арматуры и всех ее элементов регламентированы следующими методиками расчета [1, 3, 4, 5], анализ которых показал, что они не учитывают ряд факторов, влияющих на напряженно-деформированное состояние (НДС) деталей, входящих во фланцевое соединение.
Существующие методики расчета, применяемые в атомной и нефтегазовой промышленности при расчете усилий и напряжений в соединениях [1, 3], как правило, используют следующее соотношение (1):
![]()
где:
FOW – усилие начальной затяжки шпилек;
χ – коэффициент нагрузки (коэффициент податливости);
FP – гидростатическое усилие в рабочих режимах;
FT – усилие в шпильках, вызванное температурными перепадами;
FW – усилие на шпильках в рабочих условиях.
Согласно проведенному анализу, существующие методики расчета учитывают следующие факторы:
- рабочее внутреннее давление P;
- геометрические особенности деталей, входящих в сборку резьбового соединения;
- физико-механические свойства деталей (модуль продольной упругости и коэффициент линейного расширения), входящие в сборку резьбового соединения;
- среднюю температуру T на рассматриваемом участке (при определении величины усилий в шпильках, вызванных температурными перепадами).
Таким образом, существующие методики расчета справедливы для данного вида компоновки фланцевых соединений (рис. 1), где M3 – момент затяжки шпилек.
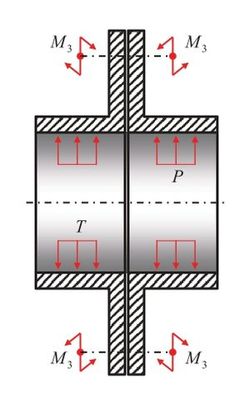
Рис. 1. Схема компоновки фланцевого соединения, рассматриваемого в существующих методиках расчета
Однако эти методики не учитывают некоторые виды механических воздействий для типов компоновок магистральных сетей, представленных на рис. 2 и рис. 3, где:
P – рабочее давление;
T – рабочая температура;
M3 – момент затяжки шпилек;
MT – весовой изгибающий и температурный моменты от трубопроводов;
FT – растягивающее усилие от трубопровода;
F3.0 – растягивающее усилие от следующей арматуры в момент полного закрытия запорного органа;
FK – растягивающие и изгибающие воздействия от трубопровода, вызванные кривизной (коленом) трубопровода.
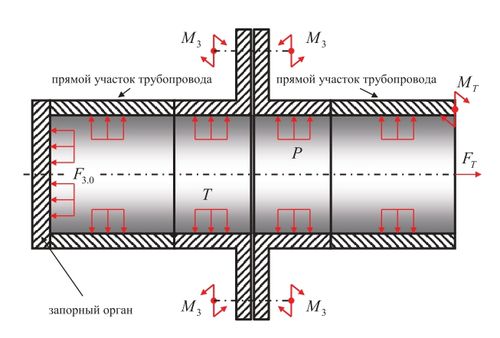
Рис. 2. Схема компоновки с присоединенной последовательно арматурой
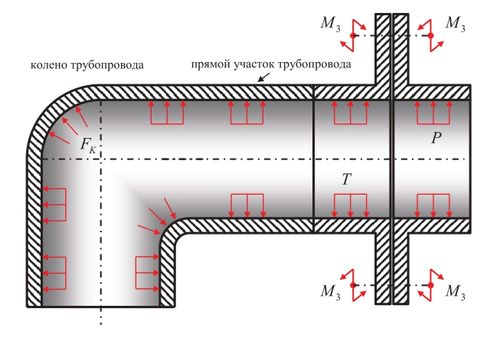
Рис. 3. Схема компоновки с коленом
Для данных типов компоновок существующие методики расчета не учитывают:
- весовые изгибающие моменты от трубопроводов;
- температурные моменты от трубопроводов;
- растягивающее воздействие от трубопровода;
- растягивающее воздействие от следующей арматуры в момент полного закрытия запорного органа (рис. 2);
- кривизну трубопровода (рис. 3);
- конвекцию и теплообмен между деталями входящими в сборку резьбового соединения.
Для учета всех дополнительных факторов внешнего воздействия на фланцевое соединение и совершенствования методики расчета необходимо решить ряд задач с использованием современных вариационных методик расчета [6, 7], теории тепло- и массообмена [7] и физики твердого тела [8].
С целью совершенствования методики расчета фланцевых соединений с учетом конструктивных особенностей трубопроводной системы необходимо решить ряд многосвязных термопрочностных и контактных задач с использованием современной теории вариационного исчисления метода конечных элементов (МКЭ). При этом прочностная задача должна учитывать:
- условие контактного взаимодействия сопрягаемых деталей;
- внешнее механическое воздействие от трубопровода;
- воздействие от трубопровода, вызванное вследствие его кривизны;
- воздействие давления среды с учетом конструктивных особенностей трубопроводных систем.
- конвективное воздействие с окружающей средой;
- контактное взаимодействие в деталях.
Решением данных задач, станет обобщенная математическая модель, способная учесть тепловое взаимодействие трубопроводной системы с окружающей средой и конструктивные особенности трубопроводной системы любой конфигурации.
Для подтверждения возможности использования в решении последующих задач метода конечных элементов (МКЭ), был проведен сравнительный анализ результатов численного и аналитического решения задачи по определению напряжений в шпильках фланцевого соединения, вызванных от действия внутреннего рабочего давления среды.
При аналитическом анализе использовалась методика расчета, указанная в [1]. Согласно данной методике, для определения напряжений в шпильках, вызванных от действия внутреннего рабочего давления среды, используется следующее соотношение:
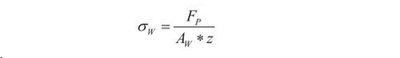
где:
FP – гидростатическое усилие в рабочих режимах;
AW – площадь поперечного сечения стержня шпильки;
z – количество шпилек, участвующих во фланцевом соединении;
σW – напряжение в шпильке в рабочих условиях.
В анализе использовались исходные данные, представленные в табл. 1.
Таблица 1.
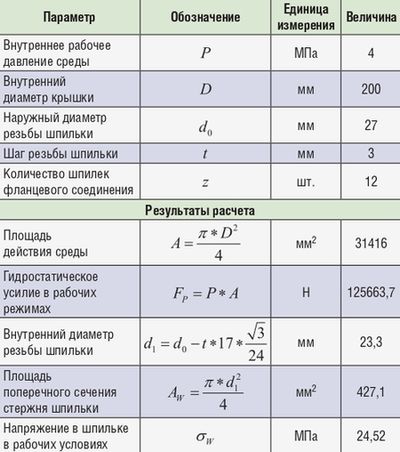
Численный анализ был проведен при помощи программного комплекса Ansys Work Bench в модуле Static Structural. Общий вид расчетной области, конечно-элементная сетка расчетной области и шпилек, заданные граничные условия представлены на рис. 4, 5, 6 и 7 соответственно.

Рис. 4. Конечно-элементная сетка расчетной области
Результаты аналитического и численного анализа представлены в сводной табл. 2.
Таблица 2.
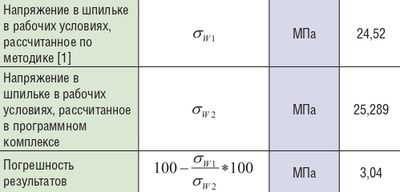
Таким образом, величина погрешности расчетов численным и аналитическим методом, свидетельствует о возможности проводить исследования с использованием современных средств вычислений, учитывая максимально возможное количество факторов, влияющих на прочность фланцевого соединения.

Рис. 5. Конечно-элементная сетка шпилек
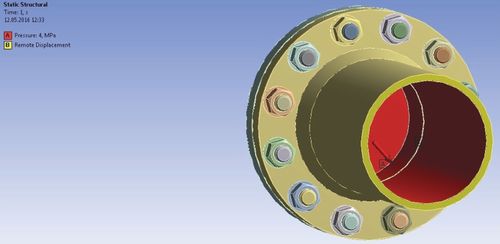
Рис. 6. Заданные граничные условия

Рис. 7. Распределение приведенных напряжений по стержню шпильки, МПа
ЛИТЕРАТУРА:
- ПНАЭ Г. 7-002-86. Нормы расчета на прочность оборудования и трубопроводов атомных энергетических установок. М.: Энергоатомиздат. 1989.
- ПНАЭ Г-7-008-89. Правила устройства и безопасной эксплуатации оборудования и трубопроводов АЭУ. – М., Энергоатомиздат, 1990.
- ГОСТ Р 52857.4-2007. Сосуды и аппараты. Нормы и методы расчета на прочность. Расчет на прочность и герметичность фланцевых соединений. М.: Стандартинформ. 2009.
- Д. Ф. Гуревич. Расчет и конструирование трубопроводной арматуры. Ленинград: Машиностроение. 1969.
- В. И. Анурьев. Справочник конструктора- машиностроителя, том 2. М.: Машиностроение. 2001.
- Зенкевич, О. Метод конечных элементов в технике / пер. с англ. под ред. Б. Е. Победри. – М.: Мир, 1975.
- Сегерлинд, Л. Применение метода конечных элементов / под ред. Б. Е. Поберди. – М.: Мир, 1979. – с. 392.
- С. П. Тимошенко, Дж. Гудьер. Теория упругости / пер. с англ. под ред. Г. С. Шапиро. М.: Наука. 1975.


